\begingroup

有没有一个合理简单的解释可以解释为什么 Bott 周期乌乌U和哦哦O分别有第 2 和第 8 周期？例如，在时长时长h– 共边定理要求n≥5​​n≥5n \geq 5有一个直观的解释，即你需要在环境流形中有足够的空间来使用惠特尼技巧将圆盘从自身上推开，这至少需要环境维度2 ⋅ 2 + 12⋅2+12\cdot 2 + 1. 是否有类似的想法或事实可以向（相对）外行人传达为什么数字 2 和 8 会出现在 Bott 周期性中？

\endgroup

1

  • 3
    \begingroup
    我一直认为这些来自实数和复数 Clifford 代数分类中的“Bott 周期性”——我倾向于认为这并不那么令人惊讶，因为它只是对应于以下事实：碳升2（三）碳升2（碳）Cl_2(\mathbb{C})和碳升8（右）碳升8（R）Cl_8(\mathbb{R})恰好同构于矩阵代数（我很乐意将其归因于机会，因为这些代数没有太多选择） – 我不确定这是否回答了你的问题，但也许你会想评论一下你会认为这条思路中的哪一类东西可以回答你的问题。
    \endgroup


    – 


最佳答案
1

\begingroup

这是 8 倍和 2 倍 Bott 周期性的直观来源之一，来自物质拓扑状态的物理学。请参阅

在物理学中，Bott 周期性决定了自由电子基本对称性的分类：反幺正对称性电视±电视±{\cal T}_\pm（时间反演对称性）和磷±磷±{\cal P}_\pm（粒子空穴对称性）和幺正对称性碳= P电视碳=磷电视{\cal C}={\cal PT}（手性对称性）。下标±±\pm区分反幺正对称性是否平方于+ 1+1+1或者− 1−1-1。

有 8 个对称类至少有一个反幺正对称性：

磷+；磷−；电视+；电视−；磷+；磷−；电视+；电视−；

{\cal P}_+;\;\;{\cal P}_-;\;\;{\cal T}_+;\;\;{\cal T}_-;

磷+，电视+；磷+，电视−；磷−，电视+；磷−，电视−；磷+，电视+；磷+，电视−；磷−，电视+；磷−，电视−；

{\cal P}_+,{\cal T}_+;\;\;{\cal P}_+,{\cal T}_-;\;\;{\cal P}_-,{\cal T}_+;\;\;{\cal P}_-,{\cal T}_-;

有 2 个对称类不具有反幺正对称性，一个具有手性对称性，一个不具有手性对称性：

碳；× ；碳；×；

{\cal C};\;\;\times;

有间隙的系统ddd维环面可以提升到维d+ 1d+1d+1通过添加一个动量分量，使间隙不会在环面上闭合。此操作以反映 Bott 周期性的方式转换对称类，如下图所示（“Bott 时钟”）。

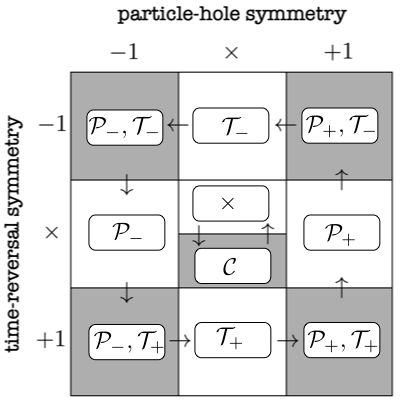
箭头表示尺寸对称性的变化ddd提升到维度d+ 1d+1d+1如果没有任何反幺正对称性，则该循环的周期为 2，如果至少有一个反幺正对称性，则该循环的周期为 8。

\endgroup